►Coreform Cubit™ Reference Manual
▼15 Appendix
►15.1 Alpha Commands
On this page:
15.1.1 Automatic Detail Suppression
15.1.2 Automatic Geometry Decomposition
15.1.3 Cohesive Elements
15.1.4 Deleting Mesh Elements
15.1.5 Feature  Size
15.1.6 Geometry Tolerant Meshing
15.1.6.9 Limitations
15.1.7 Mesh Cutting
15.1.8 Mesh Grafting
15.1.9 Optimize Jacobian
15.1.10 Randomize
15.1.11 Refine Mesh Boundary
15.1.12 Super Sizing Function
15.1.13 Test Sizing Function
15.1.14 Transition
15.1.15 Triangle Mesh Coarsening
15.1.16 Whisker Weave
2022.4-rc+26694-a523fbbc Apr 29, 2022
  top  contents  ← prev  up  next → 

15.1 Alpha Commands

Cubit™ has several functions that are currently in development and are considered "Alpha" features. These features can be can be accessed or hidden within Cubit by typing the following command:

Set Developer Commands {On|OFF}

15.1.1 Automatic Detail Suppression

Note: This feature is under development. The command to enable or disable features under development is:

Set Developer Commands {On|OFF}

Geometry models often have small features, which can be difficult to resolve in a mesh. In fact, these features are sometimes too small to see, and are revealed only when the user attempts to mesh the geometry. Automatic detail suppression identifies and removes the following types of features from the geometric model:

Details are removed using virtual geometry , which means they can be restored later if desired.

There are several stages to the automatic detail suppression process, all of which can be controlled separately by the user. Small details are identified using the command:

Detail <ref entity list> [identify] [dimension <dim> [only]]

The results are placed in a series of groups named "detail_vertices", "detail_edges", "detail_faces" and "detail_volumes". These details can be drawn or highlighted using the normal group commands:

Draw {detail_vertices | detail_edges | detail_faces | detail_volumes}

Highlight {detail_vertices | detail_edges | detail_faces | detail_volumes}

Or by using the following command:

Detail <ref entity list> draw [dimension <dim> [only]]

Details are removed automatically from the model using the command:

Detail <ref entity list> remove [dimension <dim> [only]]

The dimension option is used to identify the maximum dimension of entities examined for small detail identification (<dim> is 3, 2, 1 for volumes, surface, and curves, respectively). If the only identifier is specified, only entities of the specified dimension are examined, otherwise that dimension and all lower dimensions are examined.

In some cases, details are identified which the user would like to retain in the model; likewise, the algorithm used to identify small details sometimes misses small details the user would like removed from the model. To include or exclude geometric entities from the list of small details to be removed, the following command is used:

Detail <ref entity list> [include | exclude]

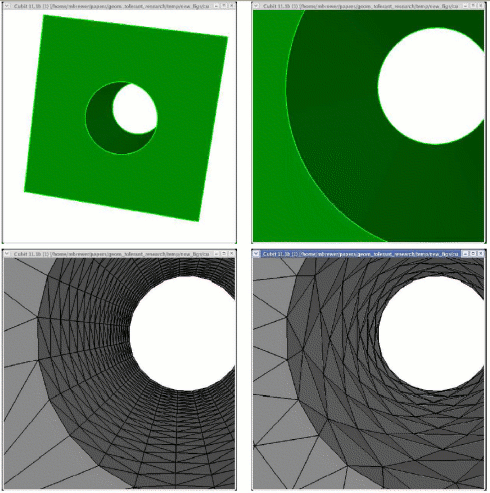
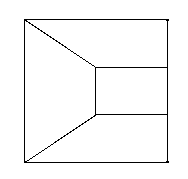
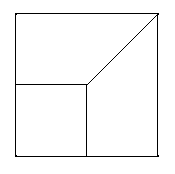
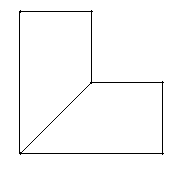
15.1.1.1 Example

Shown below is a model of a game die meshed with identical mesh size, with details included and removed.



Note: "Small" Measurement

Automatic detail suppression identifies "small" geometric entities by comparing their "size" to the mesh size assigned by the user to the entity. Anything smaller than that size is designated as a detail and put in the appropriate detail group (e.g. detail_faces, detail_edges, etc.). The size of an edge is simply its arc length; surfaces and volumes are measured using the "hydraulic diameter" (see next note).

Note: Hydraulic Diameter

The hydraulic diameter of a surface is computed as 4.0*A/P, where A is the surface area and P is the summed arc lengths of all bounding curves. For circles, the hydraulic diameter is the circle diameter; for squares, it is the length of the bounding curves. Similarly, for volumes, the hydraulic diameter is computed as 6.0*V/A, which evaluates to the diameter and bounding curve length for perfect spheres and cubes, respectively.

15.1.2 Automatic Geometry Decomposition

Note: This feature is under development. The command to enable or disable features under development is:

Set Developer Commands {On|OFF}

In many cases, model geometry includes protrusions which, when cut off using geometry decomposition, are easily meshable with existing algorithms. Cubit includes a feature-based decomposition capability, which automates this process. This algorithm operates by finding concave curves in the model, grouping them into closed loops, then forming cutting surfaces based on those loops. Although this algorithm is still in the research stage, it can be useful for automating some of the decomposition required for typical models.

To automatically decompose a model, use the command

Cut Body <body_id_range> [Trace {on|off}] [Depth <cut_depth>]

If the trace option is used, the algorithm prints progress information as decomposition progresses. The depth option controls how many cuts are made before the algorithm returns; by default, the algorithm cuts the model wherever it can.

Automatic decomposition is used to decompose the model shown in Figure 587 (left), with the results shown in Figure 587 (right). In this case, automatic decomposition performs all but one of the required cuts.

Figure 587: Model where automatic decomposition was utilized.

15.1.3 Cohesive Elements

Note: This feature is under development. The command to enable or disable features under development is:

Set Developer Commands {On|OFF}

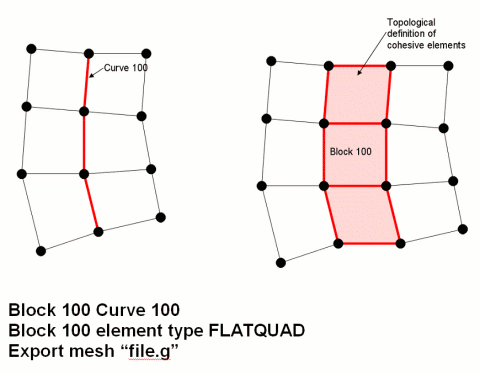
Cohesive elements are used to model things like adhesive that may lose its bond.Elements in a cohesive region originally have zero volume or area, and then expand as the simulation progresses.

Cubit supports 2D cohesive regions.Cohesive elements are implemented in Cubit as element blocks with an element type of FLATQUAD.The cohesive region is identified by assigning geometric curves to the FLATQUAD element block.When the element block is exported, each edge on the specified curves is represented in the exported file as a 4-noded quadrilateral element with zero area.The quadrilateral element is formed by duplicating each node in the original edge and then connecting the two original and two duplicate nodes to form a zero-area quadrilateral.

The image below shows how a FLATQUAD is represented in an exported mesh file.The figure on the left is how the mesh appears in Cubit.The figure on the right is how the mesh appears in the output file.Note that the figure on the right is a topological representation, not a true geometric representation.In reality, the nodes on the left side of block 100 are coincident with the nodes on the right side of block 100, causing the pink elements to have zero area.

Figure 588:

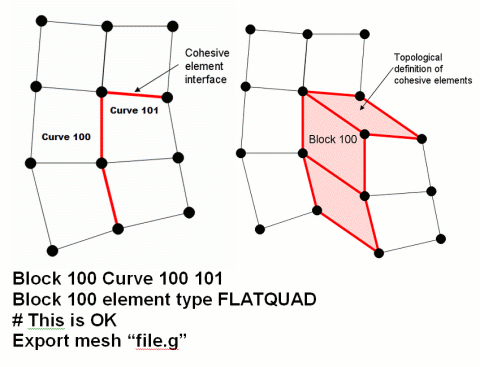
15.1.3.1 Multiple Curves in FLATQUAD Blocks

Multiple curves may be assigned to a single FLATQUAD element block, as long as the curves do not form a branching path.The figure below, for example, shows an acceptable configuration of multiple curves.

Figure 589:

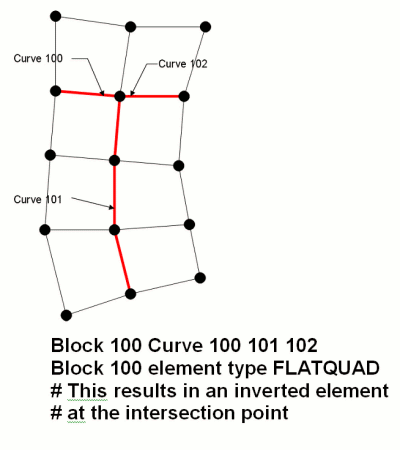
Although multiple curves may be assigned to a single cohesive block, the curves assigned to a block of type FLATQUAD must not branch.A branch occurs whenever three or more curves share a common vertex, as shown in the figure below.This will be corrected in future versions of Cubit.

Figure 590:

15.1.4 Deleting Mesh Elements

Element deletion for owned geometry is no longer available unless the developer flag is turned on. Element deletion is still available without the developer flag for free meshes. The command to enable or disable features under development is:

Set Developer Commands {On|OFF}

The following forms of the delete commands operate on meshed entities only. They allow low-level editing of meshes to make minor corrections to a mostly correct mesh. They are not designed for major modifications to existing meshes. Because Cubit’ display routines were not designed with these type of operations in mind, these commands may cause the current display of the affected entities to take an unexpected form. An appropriate drawing command can used to return the display to the desired view.

When deleting elements, the default behavior will be that the child mesh entities will be deleted when they become orphaned. For example, when a hex is deleted, if its faces, edges and vertices are no longer used by adjacent hex elements, then they will also be deleted. The no_propagate option will leave any child mesh entities regardless if they become orphaned.

The delete command removes one or more mesh entities from an existing mesh. Additional mesh entities may be deleted as well depending on the particular form of the command. Exactly which entities are removed is explained in the following descriptions.

To delete a hex or tet:

  1. In the Command Line, type set developer commands on (Set Dev On).

  2. On the Command Panel, click on Mesh.

  3. Click on Hex or Tet.

  4. Click on the Delete action button.

  5. Enter the appropriate values for Hex ID(s) or Tet ID(s). This can also be done using the Pick Widget function.

  6. Click Apply..

Delete {Hex|Tet} <range> [No_Propagate]

Deletes the specified hexes or tets. All associated tris, faces, edges, and nodes are also deleted unless the no_propagate option is given.

Delete Wedge <range>

Deletes the specified wedges. No other mesh entities are affected.

To delete a quad or tri:

  1. In the Command Line, type set developer commands on (Set Dev On).

  2. On the Command Panel, click on Mesh.

  3. Click on Quad or Tri.

  4. Click on the Delete action button.

  5. Enter the appropriate values for Quad ID(s) or Tri ID(s). This can also be done using the Pick Widget function.

  6. Click Apply..

Delete {Face|Tri} <range> [No_Propagate]

Deletes the specified faces or tris. For faces, all hexes that contain the face are also deleted. For tris, all tets that contain the tri are also deleted. All associated edges and nodes are also deleted unless the no_propagate option is given.

To delete an edge:

  1. In the Command Line, type set developer commands on (Set Dev On).

  2. On the Command Panel, click on Mesh and then Edge.

  3. Click on the Delete action button.

  4. Enter the appropriate values for Edge ID(s). This can also be done using the Pick Widget function.

  5. Click Apply..

Delete Edge <range> [No_Propagate]

Deletes the specified edges. Any associated tris, faces, hexes, and tets are also deleted. Any associated nodes are also deleted unless the no_propagate option is given.

To delete a node:

  1. In the Command Line, type set developer commands on (Set Dev On).

  2. On the Command Panel, click on Mesh and then Node.

  3. Click on the Delete action button.

  4. Enter the appropriate values for Node ID(s). This can also be done using the Pick Widget function.

  5. Click Apply..

Delete Node <range>

Deletes the specified nodes. Any associated edges, tris, faces, hexes, and tets are also deleted.

15.1.5 FeatureSize

Note: This feature is under development. The command to enable or disable features under development is:

Set Developer Commands {On|OFF}

Applies to: Curves

Summary: Meshes a curve based on its proximity to nearby geometry and size of nearby geometric features. This is an alpha feature and should be used with caution.

Syntax:

Curve <range> Scheme Featuresize

Related Commands:

Curve <range> Density <density_factor>

Discussion:

The user may also automatically bias the mesh from small elements near complicated geometry to large elements near expanses of simple geometry. Meshing a curve with scheme featuresize places nodes roughly proportional to the distance from the node to a piece of geometry that is foreign to the curve. Foreign means that the geometric entity doesn’t contain the curve, or any of its vertices (i.e. the entity’s intersection with the curve is empty). It is known that featuresize is a continuous function that varies slowly. Featuresize meshing is very automatic and integrated with interval matching. Featuresize meshing works well with paving, and in some cases with structured surface-meshing schemes (map, submap) as well.

If desired, the user may specify the exact or goal number of intervals with a size or interval command, and then the featuresize function will be used to space the nodes.

The featuresize function may also be scaled by the user to produce a finer or coarser mesh using the density command as follows:

Curve <range> Density <density_factor>

The default scaling factor or density is 1. Higher densities also reduce the transition rate of the node spacing. A density of 2 usually gives a good quality mesh. A density below about 0.5 could produce rapid transitions and poor mesh quality. The following shows an example of different density values when using the featuresize scheme.

Figure 591:

15.1.6 Geometry Tolerant Meshing

Note: This feature is under development. The command to enable or disable features under development is:

Set Developer Commands {On|OFF}

Applies to:Volumes, Surfaces

Mesh Type: Triangle, Tetrahedral, Quadrilateral

Summary:The geometry tolerant meshing algorithm takes a volume and generates a mesh by ignoring small features, gaps, slivers, and surface alignment problems in the geometry.

To create a tolerant mesh:

  1. In the Command Line, type set developer commands on (Set Dev On).

  2. On the Command Panel, click on Mesh and then Volume.

  3. Click on the Tolerant Mesh action button.

  4. Select Tolerant Mesh from the drop-down menu.

  5. Enter the appropriate values for Volume ID(s). This can also be done using the Pick Widget function.

  6. Select Triangle, Tetrahedal or Quadrilateral from the Algorithm mennu.

  7. Select FEM, New or Old.

  8. Enter the appropriate value for Tolerance Fraction.

  9. Click Apply.

Mesh Tolerant Volume <range> {Triangle|Tet|Quadrilateral} {Free} {Fraction <number>} {Fem|New|Old}

To fix or free an entity:

  1. In the Command Line, type set developer commands on (Set Dev On).

  2. On the Command Panel, click on Mesh and then Volume.

  3. Click on the Tolerant Mesh action button.

  4. Select Fix/Free Entities from the drop-down menu.

  5. Select Fix or Free.

  6. Select Volume, Surface, Curve or Vertext from the drop-down menu and enter the appropriate value.

  7. Click Apply.

Mesh Tolerant [Fix|Free] [Volume|Surface|Curve|Vertex] <range>

To create a tolerant mesh:

  1. In the Command Line, type set developer commands on (Set Dev On).

  2. On the Command Panel, click on Mesh and then Volume.

  3. Click on the Tolerant Mesh action button.

  4. Select Visualize Mesh from the drop-down menu.

  5. Enter the appropriate value for Volume ID(s). This can also be done using the Pick Widget function.

  6. Click Apply.

Mesh Tolerant Volume <range> Facet

Discussion:

Many geometric assemblies contain imperfections or small features that hinder mesh generation. These imperfections can be caused by excessive detail, data format translation errors, poorly constructed initial models and a variety of other factors. Rather than performing time-consuming geometry operations to remove these features, the geometry tolerant meshing scheme will be "tolerant" of these details, and generate a mesh that ignores features below a certain size threshold. Since there may be features under that threshold which the user desires to retain in the final mesh, there is also the option to "fix" certain geometric features so they are retained in the final mesh.

The basic approach to this method involves using the model’s facet data to create a a loose representation of the geometry using the geometry’s native kernel. This faceted representation is modified to conform to the features of the model which are either "fixed" by the user, or larger than a user-provided size. Small edges are removed from the mesh, and long edges are refined. The final mesh is created by iterating over patches of triangles from the initial mesh, and re-meshing these patches with good quality elements.

15.1.6.1 Initial Mesh Size

An initial mesh size must be input by the user before using the geometry tolerant meshing scheme. This initial mesh size is important to the final outcome. If the edge lengths are initially much smaller than the mesh size, the algorithm will have to do significant work to coarsen the mesh. On the other hand, if the mesh edges are too large, the final mesh will either not capture the geometry well, or the geometry information will, later, have to be extracted from the original model. The mesh sizing is set using the regular interval specification methods.

The sizing algorithm will assign a mesh size to each geometry element. The initial faceted mesh will be a loose approximation of these sizes.

15.1.6.2 Fixing a Geometric Entity

Before meshing the geometry, the user may wish to specify geometry that will be fixed in the final mesh. A fixed geometric entity is one that should be unchanged by the final mesh. The user may specify a volume, surface, curve, or vertex to fix. After the initial coarse representation is created, the mesh edges that belong to any of these geometric entities will be marked as fixed. One consequence of fixing an entity is that the size of the initial mesh edges that are created by the geometry kernel will be unchanged throughout the rest of the meshing process. If the faceting engine produces small mesh edges in a region, they will remain in the final mesh.

Mesh Tolerant Fix [Volume|Surface|Curve|Vertex] <range>

To reverse the effects of fixing a geometric entity, the user may "free" an entity using the following syntax

Mesh Tolerant Free [Volume|Surface|Curve|Vertex] <range>

15.1.6.3 Tolerance Fraction

The user-provided fraction controls which of non-fixed features are large enough to be included in the final mesh. It is possible for the tolerance fraction to be any number greater than zero, but in practice this number is usually less than 1. The fraction can be thought of as the percentage of the mesh size that defines a tolerable feature. After the initial faceted mesh has been created, the algorithm will loop through all of the mesh edges on the entity. Mesh edges which are smaller than the value of the (mesh size)*(tolerance fraction) will be removed if they do not belong to a fixed edge. In addition, each triangle on the surface is compared to the tolerant size to determine if it is too small. The tolerance size for a triangle is the minimum of the tolerance for the vertices. If the altitude of the triangles is shorter than that tolerance, the shortest edge of the triangle is removed. For example, if the following commands were issued:

volume 1 size 0.5
mesh tolerant volume 1 fraction 0.25


the tolerance value in the above example would be 0.5*0.25 or 0.125. Any mesh edges (from the initial faceted representation) that are smaller than 0.125 would be removed, unless fixed. Like the initial mesh size, the choice of an appropriate tolerance fraction for a given mesh size is an important to the final outcome. A larger tolerance fraction will remove more small features and possibly require you to specify more fixed edges explicitly. A smaller tolerance fraction will respect most of the original geometry, but may include features you wish to ignore.

15.1.6.4 Creating the tolerant mesh

A typical sequence of events to create a tolerant mesh would be to:

  1. Specify a mesh size

  2. Determine tolerance fraction

  3. Fix geometric entities that have features that are smaller than that mesh size * tolerance fraction using the mesh tolerant fix command

  4. Mesh the geometry using the Mesh Tolerant command

The command syntax for the meshing step is shown below

Mesh Tolerant Volume <range> {Triangle|Tet|Quadrilateral} {Free} {Fraction <number>} {Fem|New|Old}

To create just the initial faceted mesh for visualization purposes the following command may also be used

Mesh Tolerant Volume <range> Facet

The geometry tolerant scheme can also handle merged volumes and sheet bodies, and will respect boundary conditions as appropriate.

15.1.6.5 Fem/New/Old Options

The FEM/New/Old options refer to how the initial triangle surface mesh is generated. The FEM option will use Cubit’ advancing front trimesh scheme as the initial surface mesh. This is more likely to produce better quality elements, but less likely to succeed in meshing. The new and old options will both create a mesh by using the geometry engine’s facetted representaton. There is a slight variation in how the mesh is created, however. The new option will create the facet mesh for the entire volume using a method that requires no stitching, while the old option will loop over surfaces, assigning sizes and meshing them individually.

15.1.6.6 Free Mesh vs. Mesh-Based Geometry

The free option of the tolerant meshing algorithm refers to whether the final mesh is a free mesh, or if it attempts to create new mesh-based geometry to conform to the mesh. If the free option is included, the final mesh will be a free mesh, without any associated geometry. The mesh elements will be automatically placed into a group named ’tolerant_mesh_group’. All surface meshes will be placed in groups named ’mesh_from_surface_<id>’ where <id> refers to the former surface id number. If the free option is omitted, or the "Create Mesh Based Geometry" button on the GUI is checked, the algorithm will create new mesh-based geometry that resides on top of the old geometry and contains the new mesh.

15.1.6.7 Quadrilateral Surface Mesh

The quadrilateral surface meshing algorithm is based almost entirely on the triangle meshing algorithm. Only a few special steps are requred to have quadrilaterals at the final stage. The target mesh size is initially scaled by a factor of two, resulting in a slightly coarser representation of the original geometry. After the refinement step that makes the edges close to the scaled target size, each edge of the triangle is split one more time, which allows the resulting facets to be grouped into two pairs. Once this pairing has been identified, each pair is considered a quadrilateral, and the paving algorithm is used to create higher quality elements.

Figure 592: A triangle split into 4 triangles can then be paired into two quadrilaterals, the red and green shown on the right.

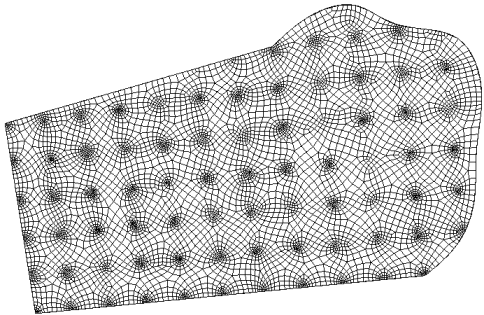
15.1.6.8 Examples

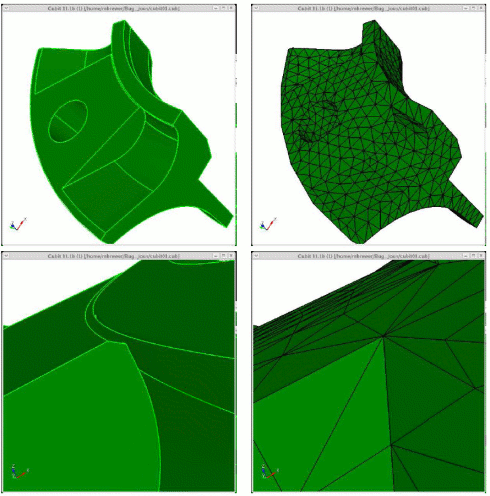
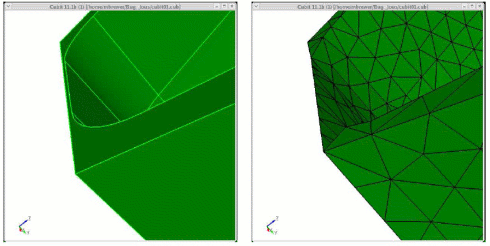
Figure 593: Demonstration of the geometry tolerant meshing algorithm to remove a small groove.

Figure 594: Removal of near-tangency between two curves

In Figure 593, the algorithm correctly detects and resolves a near tangency between two curves. However, the interior mesh edges inside the cylindrical region retain much of their original shape. This causes a slight "bulge" in the cylindrical surface. While this may not be desirable, it is the expected behavior of the algorithm.

Figure 595: Tolerant meshing performed on a simple assembly with pre-merged volumes

Figure 596: Quadrilateral shell mesh generated using geometry tolerant meshing scheme. Note that no hexahedral elements were generated.

15.1.6.9 Limitations
15.1.6.9.1 Accumulated geometric error

By performing the remeshing step on the original facets, we accumulated discretization error. The original facets are an approximation to the original surfaces, and the new facets are an approximation to the original facets. Because of this, the final mesh may not respect the original geometry, especially in areas of high curvature. However, in many cases this accumulation does not seem prohibitive. Because the facets were created to respect the original shape well, the initial discretization error is usually small.

Figure 597: Accumulation of discretization error in geometry tolerant mesh

15.1.6.9.2 Loss of Resolution due to initial faceting

If the initial faceting is coarser than the target mesh size, the refinement step is required to make the edges closer to the target size. However, for this step, we do no have a good way, yet, to maintain the geometry well. More work will be required to determine it is feasible to do this without accumulating additional error.

Figure 598: Poor resolution of geometry due to coarse initial faceting

15.1.6.9.3 Surface to Surface proximity

The current approach only removes small features that can be detected by the surface mesh. Since there are no elements filling the interior of the volume, two surfaces that are close (but have no overlapping edges) will not be flagged as small features. Regular geometry manipulation would be required in this case to tweak or remove the surfaces. Figure 599 shows an example of where the algorithm fails to recognize close surfaces as distinct surfaces.

Figure 599: Demonstration of geometry-tolerant meshing algorithm failing to recognize a thin region that has no small edges or facets

15.1.6.9.4 Mesh size on fixed geometry entities

If a geometric entity is fixed, the original facet edges on that entity are not collapsed regardless of how small, relative to the target mesh size, they may be. Therefore, in the current approach, there is no mechanism for coarsening the feature mesh edges in these regions.

15.1.7 Mesh Cutting

Note: This feature is under development. The command to enable or disable features under development is:

set developer commands {on|OFF}

The term "mesh cutting" refers to modifying an existing mesh by moving nodes to a cutting entity and modifying the connectivity of the mesh so that the original mesh fits a new geometry. The behavior of mesh cutting is intended to be similar to web cutting in that the process results in a decomposition of the original geometry. The difference is that the decomposition is performed on meshed geometry and results in the creation of virtual geometry partitions. The underlying ACIS body remains unchanged. The user has the option to determine what is partitioned during mesh cutting: the volume, the surfaces only, or nothing.

The current scope of mesh cutting is limited to cutting hex meshed volumes with planes and extended surfaces. These cutting entities are also limited in that mesh cutting will not work if they pass through a vertex at the end of more than two curves. Mesh cutting does not work on tet meshes or surface meshes.

The steps of mesh cutting include:

The following entities with the associated commands are available for mesh cutting:

15.1.7.1 Coordinate Plane

A coordinate plane can be used to cut the model, and can optionally be offset a positive or negative distance from its position at the origin.

Meshcut Volume <range> Plane {xplane|yplane|zplane} [offset <dist>]

The planar surface to be used for mesh cutting can also be previewed using the Draw Plane command.

15.1.7.2 Planar Surface

An existing planar surface can also be used to cut the model.

Meshcut Volume <range> Plane Surface <surface_id>

The planar surface to be used for mesh cutting can also be previewed using the Draw Plane command.

15.1.7.3 Plane from 3 points

Any arbitrary planar surface can be used by specifying three nodes that define the plane.

Meshcut Volume <range> Plane Node <3_node_ids>

15.1.7.4 Extended Surface

An extended surface or "sheet" can also be used for mesh cutting. In this case, the sheet is not restricted to be planar and will be extended in all directions possible. When cutting with an extended surface mesh cutting will ignore all curves and vertices of the surface. Also, the resolution of the mesh will determine how well curved surfaces are captured with meshcutting. A surface with high curvature will not be captured accurately with a coarse mesh. Note that some spline surfaces are limited in extent and may not give an expected result from mesh cutting.

Meshcut Volume <range> Sheet [Extended From] Surface <surface_id>

Note: When cutting with surfaces extended from composite surfaces the default underlying surface approximation may result in a poor final mesh for mesh cutting. This problem can be fixed using the following command:

Composite closest_pt surface <id> gme

See the discussion on composite geometry for a more detailed description of this command.

15.1.7.5 Meshcut Options

The following options can be used with all the meshcut commands:

[PARTITION VOLUME|partition surface|no_partition]

: By default, mesh cutting will create virtual partitions of the volume being cut to match the cutting entity. This option allows mesh cutting to also create only the surface partitions or create no partitions for the volume or surfaces.

[no_refine]: This option tells mesh cutting not to refine the mesh around the cutting entity.

[no_smooth]: This option tells mesh cutting not to perform the final smoothing step after the cut has been made.

15.1.7.6 Meshcutting Scope

The following is a list of the current scope and limitations of meshcutting.

15.1.7.7 Meshcutting Example

The figures below show an example of mesh cutting. Figure 600 shows the body that will be meshed. This body is a brick with intersecting through-holes. The steps to create a mesh for this body are listed below.

smooth_brick.gif

Figure 600: The original, unmeshed body

Step 1: Create a starting mesh. Figure 601 below shows the starting mesh for this problem. The commands for this mesh are:

Cubit> create brick x 10
Cubit> create cylinder radius 3 z 15
Cubit> subtract 2 from 1
Cubit> volume 1 scheme sweep
Cubit> volume 1 size .75
Cubit> mesh volume 1

start_mesh.gif

Figure 601: The starting mesh

Step 2: Create a cutting entity. Figure 602 shows the volume that will be used to cut the mesh. The commands are:

Cubit> create cylinder radius 2 z 15
Cubit> rotate body 3 about x angle 90

mesh_cyl.gif

Figure 602: The starting mesh and cutting entity

Step 3: Cut the mesh. Figure 603 shows the new mesh after the original mesh has been cut. At this point we have 3 meshed volumes. The commands for this step are:

Cubit> meshcut vol 1 sheet surface 13
Cubit> draw volume 1 4 5

cut_1.gif

Figure 603: The mesh after meshcutting

Step 4: Final step. Figure 604 shows the final mesh after the mesh of the mesh of the two extra volumes is deleted. The commands are:

Cubit> delete mesh vol 4 5 propagate
Cubit> draw volume 1

cut_2.gif

Figure 604: Final mesh after deleting unneeded elements

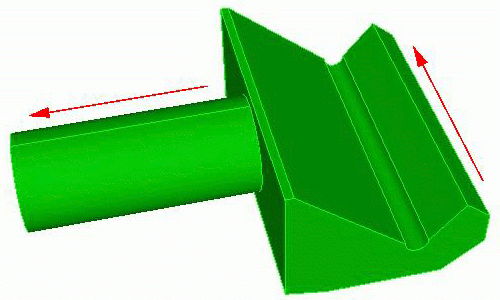
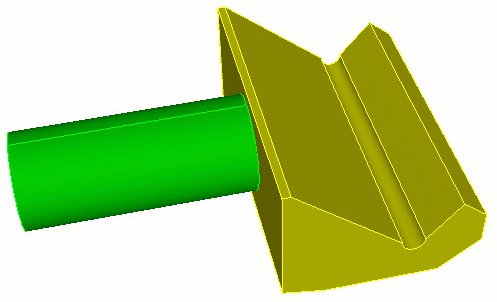
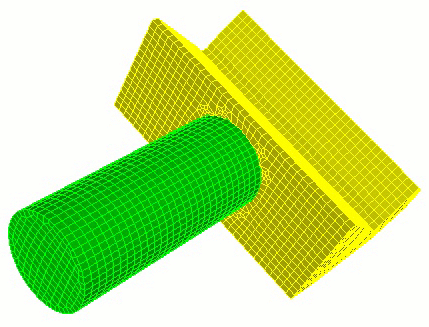
15.1.8 Mesh Grafting

Note: This feature is under development. The command to enable or disable features under development is:

Set Developer Commands {On|OFF}

Grafting is used to merge a meshed surface with a dissimilar unmeshed surface. In the process, the location of the nodes on the meshed surface will be adjusted to fit to the bounding curves of the unmeshed surface and the connectivity of the original mesh may be changed to improve the final quality of the mesh. This allows an unmeshed volume to be attached–or grafted–onto a meshed volume. Grafting is particularly useful for models that have intersecting sweep directions (see example below).

The command syntax for grafting is:

Graft {Surface <range> | Volume <id>} onto Volume <id> [no_refine] [no_smooth]

The Graft command will check that the second volume is meshed. It then searches for surfaces on the second volume that overlap with the other volume or range of surfaces that is specified. If overlapping surfaces are found the mesh will then be adjusted on the second volume and after any needed imprinting is done the overlapping surfaces will be merged together.

15.1.8.1 Grafting Options

[no_refine]: This option tells grafting not to modify the connectivity of the original mesh. The mesh is still adjusted to fit the boundary of the branch surface but no new elements are added.

[no_smooth]: This option tells grafting not to perform the final smoothing of the modified surface or volume mesh.

15.1.8.2 Grafting Scope

The following is a list describing the current scope and limitations of grafting:

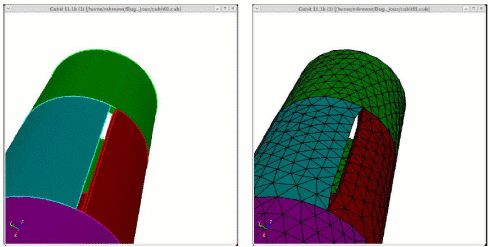
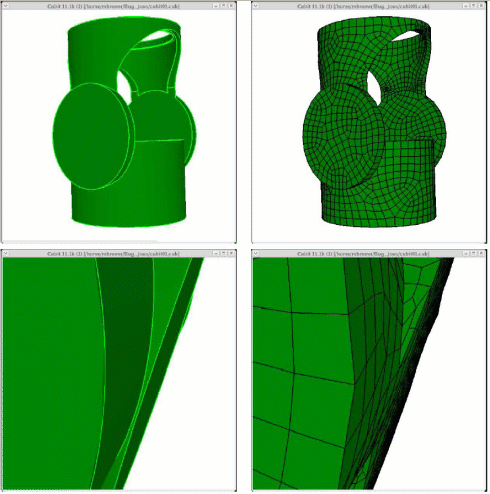
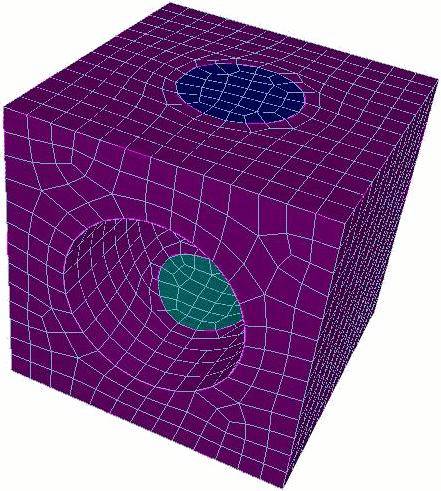
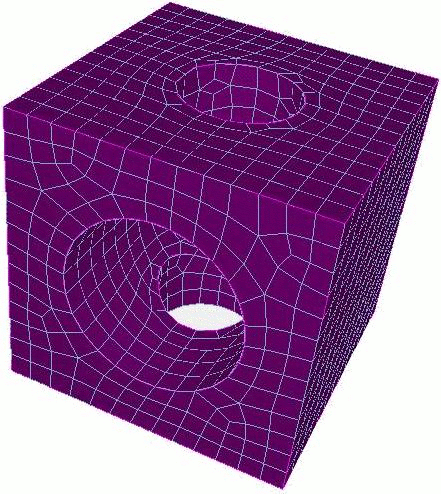
Grafting Example

This example shows the four basic steps of grafting:

  1. Partition the geometry (optional).

  2. Mesh the trunk volume.

  3. Graft the branch volume onto the trunk volume.

  4. Mesh the branch volume.

Step 1: Partition the geometry

Figure 605 shows the model that will be meshed. The arrows in the figure show the two intersecting sweep directions. Figure 606 shows the model decomposed for grafting.

Figure 605: A model with two intersecting sweep directions.

Figure 606: The model decomposed for grafting

Step 2: Mesh the trunk volume.

Figure 607 shows the mesh of the trunk volume. At this point the mesh on the trunk surface adjacent to the branch surface is a structured mesh that does not align with the boundary of the branch surface. The trunk and branch surfaces are two separate surfaces.

Figure 607: Meshed trunk volume.

Step 3: Graft the branch onto the trunk

Figure 608 shows the trunk surface after it has been modified to fit the branch surface. At this point the two surfaces have been merged together.

Figure 608: Trunk surface after grafting.

Step 4: Mesh the branch volume.

The final mesh is shown in Figure 609.

Figure 609: Final mesh

15.1.9 Optimize Jacobian

Note: This feature is under development. The command to enable or disable features under development is:

Set Developer Commands {On|OFF}

Applies to: Volume meshes

Summary: Produces locally-uniform hex meshes by optimizing element Jacobians

Syntax:

Volume <range> Smooth Scheme Optimize Jacobian [param]

Discussion:

The Optimize Jacobian method minimizes the sum of the squares of the Jacobians (i.e., volumes) attached to the smooth node. Meshes smoothed by this means tend to have locally-uniform hex volumes.

The parameter <param> has a default value of 1, meaning that the method will attempt to make local volumes equal. The parameter, which should always be between 1 and 2 (with 1.05 recommended), can be used to sacrifice local volume equality in favor of moving towards meshes with all-positive Jacobians.

15.1.10 Randomize

Note: This feature is under development. The command to enable or disable features under development is:

Set Developer Commands {On|OFF}

Applies to: Curve, Surface and Volume meshes

Summary: Randomizes the placement of nodes on a geometry entity

Syntax:

{Surface|Volume} <range> Smooth Scheme Randomize [percent]

Discussion: This scheme will create non-smooth meshes. If a percent argument is given, this sets the amount by which nodes will be moved as a percentage of the local edge length. The default value for percent is 0.40. This smooth scheme is primarily a research scheme to help test other smooth schemes.

15.1.11 Refine Mesh Boundary

Note: This feature is under development. The command to enable or disable features under development is:

set developer commands {on|OFF}

Boundary effects to be modeled in the analysis code frequently require a refined mesh near a specific surface. Cubit provides this capability with the Refine Mesh Boundary command.This command is similar to the Refine Mesh Volume Feature command except that it can insert multiple sheets of hexes near the specified surface.

Refine Mesh Boundary Surface <range> Volume <id> {Bias <double>} {First_delta <double> | Thickness <double>} [Layer <num_layers=1>] [SMOOTH|No_smooth]

With this command num_layers of hexes can be inserted at the first interval from the specified surface. A bias factor indicating the change in element size must be specified. You must also indicate a first_delta or thickness which represents the distance to the first inserted layer. The mesh in Figure 610 with bias 1.0 and first_delta of 5. The default smooth option provides the capability to smooth the mesh following the refinement procedure.

Figure 610: Example of Boundary Surface Refinement

15.1.12 Super Sizing Function

Note: This feature is under development. The command to enable or disable features under development is:

Set Developer Commands {On|OFF}

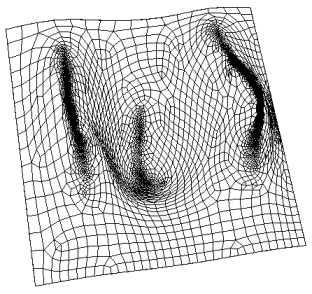
The super sizing function computes both the Curvature and the Linear function and takes the smaller value of the two. This is an alpha feature and should be used with caution. The following is an example of Super element sizing.

Figure 611: NURB mesh with super sizing function, 34 by 16 density

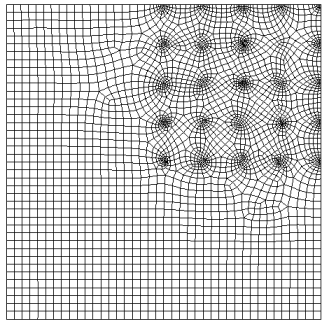
15.1.13 Test Sizing Function

Note: This feature is under development. The command to enable or disable features under development is:

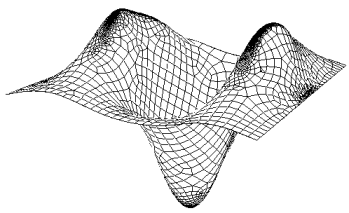
set developer commands {on|OFF}

The test sizing function is a hard wired numerical function used to demonstrate the transitional effect of sizing function-based and adaptive paving. The function is a periodic function which is repeated in 50x50 unit intervals on a 2D surface in the first quadrant (x > 0, y > 0, z = 0). This is an alpha feature and should be used with caution. An example of a surface meshed with this sizing function is shown in Figure 612 and Figure 613.

Figure 612: Test sizing function for square geometry

Figure 613: Test sizing function for spline geometry

[}

15.1.14 Transition

Note: This feature is under development. The command to enable or disable features under development is:

set developer commands {on|OFF}

Applies to: Surfaces

Summary: Produces a specified transition mesh for specific situations

Syntax:

Surface <range> Scheme Transition {Triangle|Half_circle|Three_to_one|Two_to_one|Convex_corner|Four_to_two} [Source Curve <id>] [Source Vertex <id>]

Discussion:

The transition scheme supplies a set of transition primitives which serve to transition a mesh from one density to another across a given surface. The six transition sub-types are demonstrated here.

Scheme Transition triangle creates four quads in a triangle that has sides of three, two, and one intervals.

Scheme Transition half_circle creates three intervals on the flat and three on the curved part of the half-circle, then creates four quads in the surface.

Scheme Transition three_to_one creates four quads on a rectangular surface that has intervals of three, one, one, and one on its sides.

Scheme Transition two_to_one creates three quads on a rectangular surface that has intervals of two, two, one and one on its sides :

Scheme Transition convex_corner takes a six-sided block with a convex corner and connects that inner corner to the opposite one, creating two quads on the surface.

Scheme Transition four_to_two creates seven quads on a rectangular surface that has intervals of four, two, two, and two on its sides.

The user also has the option of specifying a source curve and/or a source vertex. The rules for these specifications are as follows

15.1.15 Triangle Mesh Coarsening

Note: This feature is under development. The command to enable or disable features under development is:

Set Developer Commands {On|OFF}

Cubit provides the capability for coarsening triangle surface meshes. Triangle coarsening uses a technique known as edge collapsing to coarsen a mesh. With this technique, triangle edges are selectively eliminated from the mesh until the specified criteria have been met. The following commands will coarsen an existing triangle surface mesh:

Coarsen {Node|Edge|Tri} <range> {Factor|Size <double> [Bias <double>]} [Depth <int>|Radius <double>] [Sizing_Function] [no_smooth]

Coarsen {Vertex|Curve|Surface} <range> {Factor|Size<double> [Bias<double>]} [Depth<int>|Radius<double>] [Sizing_Function] [no_smooth]

Important: These commands are currently implemented only for triangle shaped elements.

To use these commands, first select mesh or geometric entities at which you would like to perform coarsening. Coarsening operations will be applied to all mesh entities associated with or within proximity of the entities. The all keyword may be used to uniformly coarsen all triangles in the model.

Following is a description of each of the coarsen options:

factor

Defines the approximate size relative to the existing edge lengths for which the coarsening will be applied. For example, a factor of 2 will attempt to make every edge length within the specified region approximately twice the size. A factor of 3 will make everything three times the size. Valid input values for factor must be greater than 1. Figure 614 shows an example where a coarsening factor of 2 was applied

coarsen_tri.gifcoarsen_tri2.gif

Figure 614: Example of coarsening all triangles with a factor of 2.

size, bias

The Size and Bias options are useful when a specific element size is desired at a known location. This might be used for locally coarsening around a vertex or curve. The Bias argument can be used with the Size option to define the rate at which the element sizes will change to meet the existing element sizes on the model. Valid input values for Bias are greater than 1.0 and represent the maximum change in element size from one element to the next. Since coarsening is a discrete operation, the Size and Bias options can only approximate the desired input values. This may cause apparent discontinuities in the element sizes. Using the default smooth option can lessen this effect. It should also be noted that the Size option is exclusive of the Factor option. Either Factor or Size can be specified, but not both.

depth

The Depth option permits the user to specify how many elements away from the specified entity will also be coarsened. Default Depth is 1.

tri_coarsen_depth0.giftri_coarsen_depth1.gif

Figure 615: Coarsening performed at a node with factor = 3 and depth = 3

radius

Instead of specifying the number of elements to describe how far to propagate the coarsening, a real Radius may be entered.

sizing function

Coarsening may also be controlled by a sizing function. Cubit uses sizing functions to control the local density of a mesh. Various options for setting up a sizing function are provided, including importing scalar field data from an exodus file. In order to use this option, a sizing function must first be specified on the surface on which the coarsening will be applied. See Adaptive Meshing for a description of how to define a sizing function.

no_smooth

The default mode for coarsening operations is to perform smoothing after coarsening the elements. This will generally provide better quality elements. In some cases it may be necessary to retain the original node locations after coarsening. The no_smooth option provides this capability.

15.1.16 Whisker Weave

Note: This feature is under development. The command to enable or disable features under development is:

set developer commands {on|OFF}

}

Applies to: Volumes

Summary: Research algorithm for all-hexahedral meshing of arbitrary 3D volumes

Syntax:

Volume <range> Scheme Weave

Related Commands:

Pillow Volume <range>

{Volume|Surface|Curve} <range> Mesh [Fixed|Free]

Set AutoWeaveShrink [on|off]

Set Statelist [on|off]

Discussion:

Whisker Weaving (Tautges, 96; Tautges, 95; Folwell, 98) is a volume meshing algorithm currently being researched and is not released for general use. However, daring users may find the current form of the algorithm useful for mostly-convex geometries.

Whisker Weaving holds the promise of being able to fill arbitrary geometries with hexahedra that conform to a fixed surface mesh. The algorithm is based on the rich information contained in the Spatial Twist Continuum (STC) (Murdoch, 95), which is the grouping of the dual of an all-hexahedral mesh into an arrangement of surfaces called sheets. Given a bounding quadrilateral surface mesh, Whisker Weaving constructs sheets advancing from the boundary inward. The sheets are then modified so that the arrangement dualizes to a well defined hexahedral mesh. Once the primal hex-mesh is generated, interior node positions are generated by smoothing.

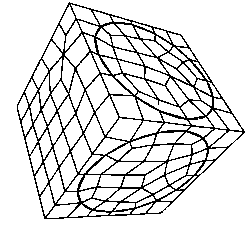
Examples of meshes generated using the whisker weaving algorithm are shown in the following figure.

Figure 616: Some simple Whisker Weaving meshes with good quality

15.1.16.1 Whisker Weaving Basic Commands

The basic steps for meshing a volume with Whisker Weaving are the following:

Set the meshing scheme for the volume to weave

Volume <range> Scheme Weave

Mesh the volume, which generates hexes

Mesh Volume <range>

Pillow the volume to remove certain additional degenerate hexes

Pillow Volume <range>

and typically, smooth the mesh to improve quality, e.g.

Volume <range> Smooth Scheme Condition Number

smooth volume <range>

15.1.16.2 Whisker Weaving Options

Currently, Whisker Weaving relies on being able to perturb the bounding quadrilateral mesh. However, a bounding surface’s mesh will not be changed if it is contained in another volume that is already meshed.

The user may also explicitly prevent Whisker Weaving from changing a bounding mesh by fixing it with the following command:

{Volume|Surface|Curve} <range> Mesh [Fixed|Free]

The user may select an optional control strategy that doesn’t change the surface mesh by setting autoweaveshrink off, and setting statelist on with the following commands:

Set AutoWeaveShrink [on|off]

Set Statelist [on|off]

Numerous developer commands are available for stepping through the algorithm, examining results, and toggling options. These are available via the command line help but are not detailed here.

  top  contents  ← prev  up  next →